頭の痛い仕事でひとしきり唸り終えた後は、「インドアトレーナーに最適な負荷装置」はどんなもんなんだろう?とか優雅に思索を巡らせたりする今日この頃のメモ。全然優雅じゃねー。
一定速度で走る自転車にかかる抵抗は
- 空気抵抗
- 転がり抵抗
- 勾配抵抗
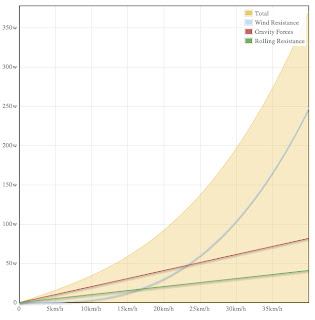
の3つで、それぞれの比率は速度や勾配に応じて変化する。3つの走行抵抗の比率の変化を勾配0、1、3、6、12、18%ごとにプロットしてみた。
横軸が速度[km/h]で縦軸が仕事率[W]。青が空気抵抗[W]、赤が勾配抵抗[W]、緑が転がり抵抗[W]。黄は3つを合算した全走行抵抗[W]。抵抗は[N]なんだけど、比較しやすいように速度[m/s]をかけて仕事率[W]でプロットしてる。
勾配0だと空気抵抗が支配的だけど、1%でも勾配がつくと3抵抗がそれぞれトントンになってくる。さらに勾配がつくとすぐに勾配抵抗が支配的になる。そして源泉徴収される税金のように転がり抵抗がどんな場面でもついてまわってる。
抵抗として発生する力[N]は
空気抵抗[N] = 0.5 x 大気密度[kg/m^3] x 空気抵抗係数 x 速度[m/s]^2
転がり抵抗[N] = 質量[kg] x 重力加速度[m/s^2] x 転がり抵抗係数
勾配抵抗[N] = 質量[kg] x 重力加速度[m/s^2] x sin arctan(勾配[%]/100)
上記3つの力に速度[m/s]をかければ必要な仕事率[Nm/s=J/s=W]を得られる。質量[kg]が軽ければ余剰パワーをつかってより素早く(大きな加速度[m/s^2]で)加速できる。
各グラフは上記の式につぎのパラメータで計算したもの。
- 質量(ライダー+自転車+装備品): 75[kg]
- 重力加速度: 9.81[m/s^2]
- 大気密度: 1.226[kg/m^3]
- 空気抵抗係数: 0.295
- 転がり抵抗係数: 0.005
「自転車競技は空気抵抗との戦い」なのは事実だと思うのだけど、ほんのちょっと勾配がついただけで「重力との戦い」に変わっていく。あー「体重との戦い」って言った方がいいかも。もちろん下り勾配もあるロードレースとかなら総合すると±0で「空気抵抗との戦い」なのかもしれない。
勾配のある場面でコースティングすると急激に失速するのは、速度に関係なく勾配抵抗がかかるから。平地では速度に応じて空気抵抗が小さくなるので緩やかに失速する。(あたりまえだけど)慣性による運動エネルギーは坂でも平地でも同じ。
本当にリアルなローラー台を作ろうとすると、こーいう場面に応じた速度・抵抗の変化をシミュレートする必要があるわけで、平地も任意の坂もリアルにしようとするなら、
- マグネットやブレーキを電子制御する方式
- フルード(空気抵抗)と切り替え式マグネット(勾配抵抗+転がり抵抗)のハイブリット
のどちらかになるかな。もちろん上記以外にも遠心力でマグネットの距離を可変させたりする他の方式もある。いずれの方式も製品として流通してる。さらに下り勾配もシミュレートしようってもんなら、東京体育館の全身持久力測定でおなじみStrength Ergo 8みたくサーボモーターでアシストしないといかんのか(それは流石に不要か...いや下りスプリントとか色々....いやいやもちつけ)
んまぁ、速度対負荷の推移よりも、ライダー+自転車+装備の慣性質量に相当する慣性モーメントをもったフライホイールがよほど重要なのかかもしれないけどどどど。